|
Հանրահաշիվ
Սահմանում
Այն թվերը, որոնք առաջանում են համրանքի ժամանակ կոչվում են բնական թվեր:
Բնական թվերի բազմությունը նշանակուվում էN տառով:
Սահմանում
Բնական թվերը, նրանց հակադիրները և զրոն կոչվում են ամբողջ թվերի բազմություն:
Բնական թվերի բազմությունը նշանակուվում էZ տառով:
Սահմանում
Բոլոր 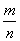 տեսքի թվերը, որտեղ m ամբողջ է, n – ը` բնական, կոչվում են ռացիոնալ թվեր: տեսքի թվերը, որտեղ m ամբողջ է, n – ը` բնական, կոչվում են ռացիոնալ թվեր:
Բնական թվերի բազմությունը նշանակուվում է Q տառով:
Սահմանում
Այն թվերը, որոնք ներկայացվում են ամբողջ ոչ պարբերական կոտորոկի տեսքով կոչվում են իռացիոնալ թվեր:
Օրինակ 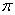 =3.141592753… =3.141592753…
Ահա և հեշտ և սիրով սովորեցրի մի անսովոր խրթին թիվ:
Սահմանում
Ռացիոնալ և իռացիոնալ թվերը միասին կազմում են իրական թվերի բազմությունը:
Բնական թվերի բազմությունը նշանակուվում էR տառով:
Թեորեմ
Պարզ պարբերական տասնորդական կոտորակը հավասար է մի կոտորակի, որի համարիչում գրված է պարբերությունում եղած թիվը, իսկ հայտարարում այնքան ինը, որքան թիվ կա պարբերության մեջ:
Օրինակ`
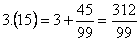
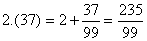
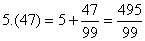
Թեորեմ
Խառը անվերջ պարբերական տասնորդական կոտորոկը հավասար է մի կոտորակի, որի համարիչում գրված է մինչև երկրորդ պարբերությունը եղած թվից հանած մինչև առաջին պարբերությունը եղած թիվը, իսկ հայտարարում այնքան ինը, որքան թիվ կա պարբերության մեջ և այնքան զրո, որքան թիվ կա մինչև պարբերությունը:
Օրինակ` 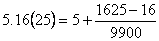
Սահմանում
Բնական թվերը կոչվում են պարզ, եթե բաժանվում են միայն իր և 1-ի վրա:
Օրինակ` 2; 3; 5; 7; 11; 13;…
Սահմանում
Բնական թվերը կոչվում են բաղադրյալ, եթե բացի իրենից և մեկից ունեն նաև այլ բաժանարար:
Օրինակ` 4; 6; 15; 144; 225; …
Սահմանում
Տրված թվի բաժանարար կոչվում է այն թիվը, որի վրա տրված թիվը բաժանվում է առանց մնացորդի:
Օրինակ` 64-ի բաժանարարներն են` 2; 4; 8; 16; 32; 64 :
Սահմանում
Տրված թվի բազմապատիկ է կոչվում այն թիվը, որը տրված թվի վրա բաժանվում է առանց մնացորդի:
Օրինակ` 6-ի բազմապատիկներն են 6; 12; 18; 24; 30; 36 :
Հատկություն
Բաժանարարների բազմությունը վերջավոր է, բազմապատիկներինը` անվերջ:
Սահմանում
Երկու բնական թվեր միմյանց նկատմամբ կոչվում են փոխադարձաբար պարզ, եթե չունեն ընդհանուր բաժանարար:
Օրինակ` 25 և 16; 11 և 13; 9 և 4
Թեորեմ
Բնական թիվը բաժանվում է երկուսի վրա, եթե վերջանում է զրոյով կամ զույգ թվանշանով:
Թեորեմ
Բնական թիվը բաժանվուն է 3-ի վրա, եթե նրա թվանշանների գումարը բաժանվում է 3-ի վրա:
Օրինակ` 506841= 5 + 0 + 6 + 8 + 4 + 1 = 24 : 3 = 8
Թեորեմ
Բնական թիվը բաժանվում է 4-ի վրա, եթե այդ թվի վերջին երկու թվանշաններով կազմված թիվը բաժանվում է 4-ի:
Օրինակ` 3058924 24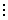 4 4
Թեորեմ
Բնական թիվը բաժանվում է 5-ի վրա, եթե այն վերջանում է 0-ով կամ 5-ով:
Թեորեմ
Եթե թիվը բաժանվում է 2-ի և 3-ի վրա, ապա բաժանվում է 6-ի վրա:
Թեորեմ
Եթե թիվը բաժանվում է 2-ի և 4-ի վրա, ապա բաժանվում է 8-ի վրա:
Թեորեմ
Եթե թիվը վերջանում է երկու զրոներով կամ 25-ով, ապա բաժանվում է:
Օրինակ` 716000; 81025
Թեորեմ
Մի քանի թվերի ամենափոքր ընդհանուր բազմապատիկը գտնելու համար թվերը վերլուծում ենք պարզ արտադրիչների , վերցնում ենք ընդհանուր արտադրիչները մեծ ցուցիչով և կատարում ենք բազմապատկում:
Օրինակ` Գտնենք 32 և 48 ամենափոքր ընդհանուր բազմապատիկը
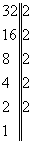  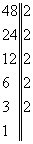
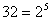 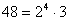
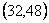 ափըբ= ափըբ= 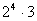
Թեորեմ
Մի քանի թվերի ամենամեծ ընդհանուր բաժանարարը գտնելու համար թվերը վերլուծում ենք պարզ արտադրիչների , վերցնում ենք ընդհանուր արտադրիչները փոքր ցուցիչով և կատարում ենք բազմապատկում:
Օրինակ` Գտնենք 2496 և 1236 ամենամեծ ընդհանուր բաժանարարը
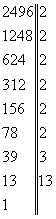 
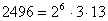 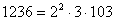
(2496,1236)ամըբ=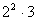 =12 =12
Կրճատ բազմապատկման բանաձևեր
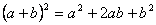 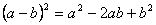 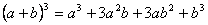 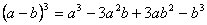 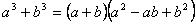 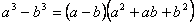 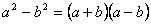
Աստիճանի հիմանակ հատկությունները
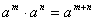 , , 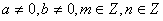
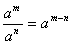 , , 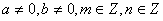
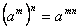 , , 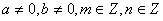
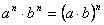 , , 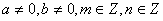
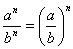 , , 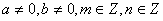
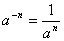 , , 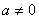
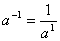 , , 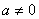
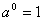 , , 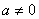
-
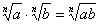 , , 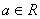 , , 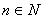 , , 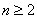
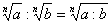 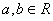 , ,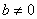 , , 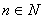 , , 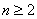
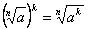
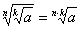
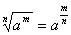 , , 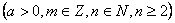
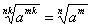 , , 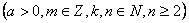
Իրական ցուցիչով աստիճանների հատկությունները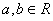 , ,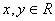
- Եթե x>y, ապա
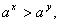 երբ երբ 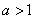
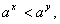 երբ երբ 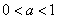
- Եթե a>b>0, ապա
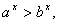 երբ երբ 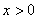
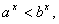 երբ երբ 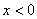
Նյուտոնի երկանդամ կամ բինոմ
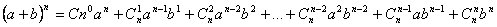
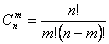
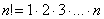
Ընդունված է` 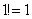
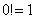
Քառակուսային եռանդամ
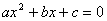 տեսքի հավասարումը, որտեղ տեսքի հավասարումը, որտեղ 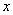 -ը փոփոխական է, -ը փոփոխական է, 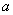 -ն, -ն,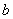 -ն, -ն,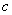 -ն որևէ իրական թվեր են ( -ն որևէ իրական թվեր են (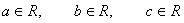 ), ընդ որում ), ընդ որում 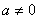 , կոչվում է քառակուսայինհավասարում: , կոչվում է քառակուսայինհավասարում:
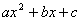 բազմանդամը (քառակուսային հավասարման ձախ մասը) կոչվում է քառակուսայինեռանդամ: բազմանդամը (քառակուսային հավասարման ձախ մասը) կոչվում է քառակուսայինեռանդամ:
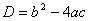 արտահայտությունը կոչվում է արտահայտությունը կոչվում է 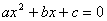 քառակուսային հավասարման տարբերիչ (կամ դետերմինանտ): քառակուսային հավասարման տարբերիչ (կամ դետերմինանտ):
Քառակուսային հավասարումների լուծումը
Եթե 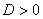 , ապա ունի երկու արմատ` , ապա ունի երկու արմատ`
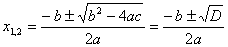 : :
Եթե 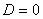 , ապա ունի մեկ արմատ` , ապա ունի մեկ արմատ` 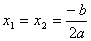 : :
Եթե 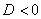 , ապա արմատ չունի` , ապա արմատ չունի` 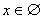 : :
Մասնավոր դեպքում, երբ b-ն զույգ է (այսինքն, 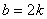 կամ կամ 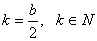 ) և ) և 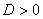 , ապա հարմար է օգտվել հետևյալ բանաձևից` , ապա հարմար է օգտվել հետևյալ բանաձևից`
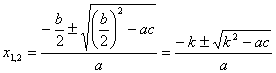
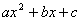 քառակուսայի եռանդամի վերլուծումը արտադրիչների` քառակուսայի եռանդամի վերլուծումը արտադրիչների`
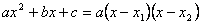 , որտեղ , որտեղ 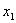 -ը և -ը և 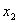 -ը եռանդամի արմատներն են: -ը եռանդամի արմատներն են:
Բերվածտեսքիքառակուսայինհավասարում
Սահմանում Եթե 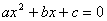 ( (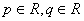 ) քառակուսային հավասարման մեջ ) քառակուսային հավասարման մեջ 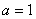 ,ապա կստացվի ,ապա կստացվի 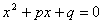 տեսքի հավասարում, որը կոչվում է բերված տեսքի քառակուսային հավասարում: տեսքի հավասարում, որը կոչվում է բերված տեսքի քառակուսային հավասարում:
Բերված տեսքի քառակուսային հավասարումների լուծումը:
Եթե 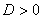 ( (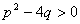 ), ապա ունի երկու արմատ` ), ապա ունի երկու արմատ`
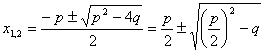 : :
Եթե 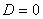 ( (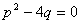 ), ապա ունի մեկ արմատ` ), ապա ունի մեկ արմատ`
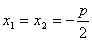 : :
Եթե 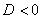 ( (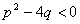 ), ապա արմատ չունի` ), ապա արմատ չունի` 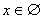 : :
Վիետի թեորեմը
Եթե 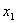 -ը և -ը և 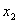 -ը -ը 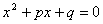 բերվածտեսքի քառակուսային հավասարման արմատներն են, ապա բերվածտեսքի քառակուսային հավասարման արմատներն են, ապա
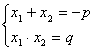
Վիետի թեորեմի հակադարձ թեորեմը
Եթե 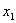 և և 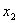 թվերի համար կատարվում են թվերի համար կատարվում են 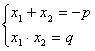 հավասարությունները, ապա հավասարությունները, ապա
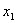 -ը և -ը և 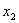 -ը -ը 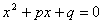 հավասարման արմատներն են: հավասարման արմատներն են:
|

